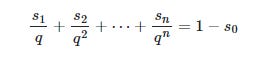Attention: As of January 2024, We have moved to counting-stuff.com. Subscribe there, not here on Substack, if you want to receive weekly posts.
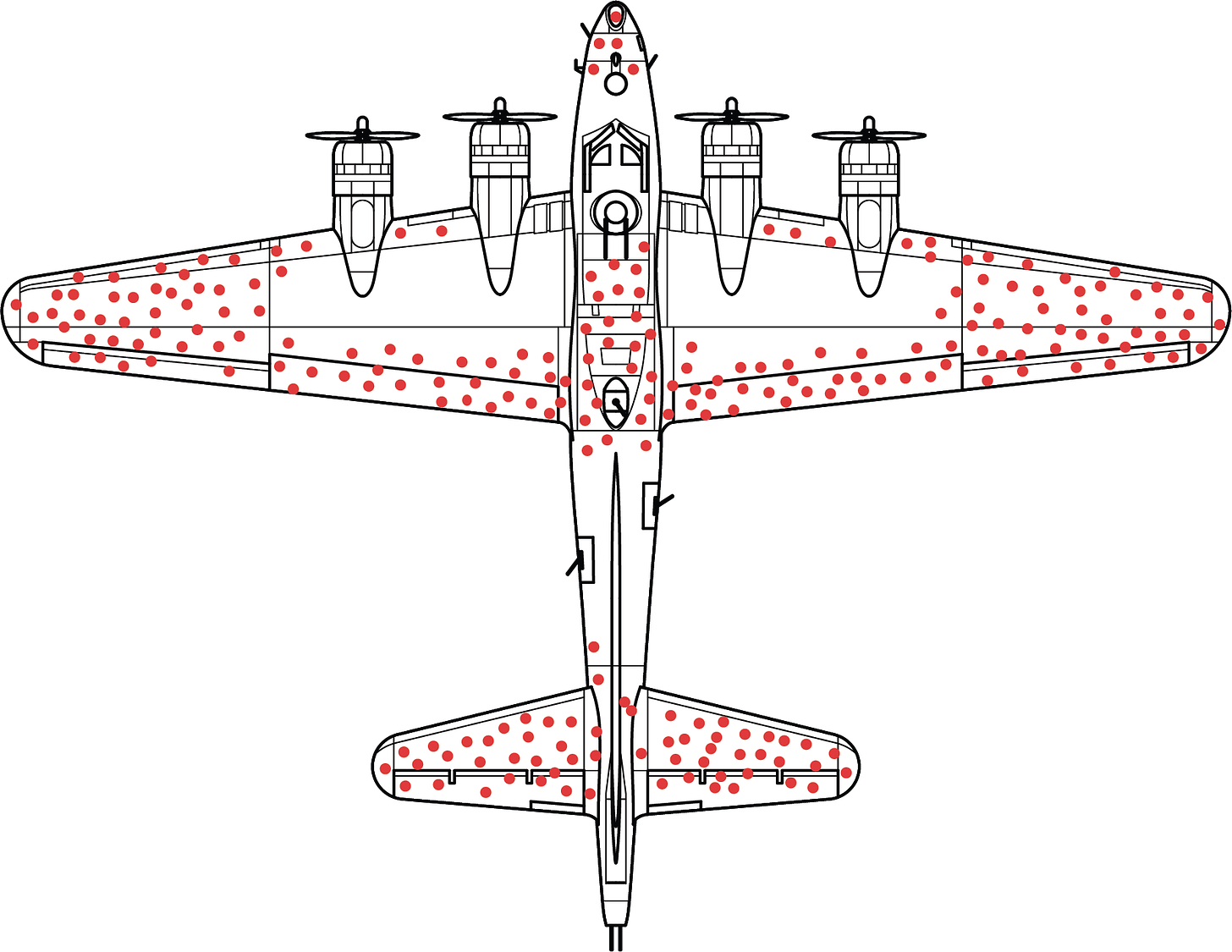
The past week, I designed a thing. Originally I had wanted to make an enamel pin for the “survivorship bias” airplane for myself and was fighting with Illustrator to get the design to work. Along the way, as I tweeted my frustration at getting paths to fill in correctly, someone commented that they’d love a T-shirt with it.
What? There’s no t-shirt of this design? Apparently there wasn’t… until now.
I created a version of the above design so that it would fit onto a shirt design while originally wanting to make an enamel pin of it. It’s available for order off of RedBubble’s print-to-order system.
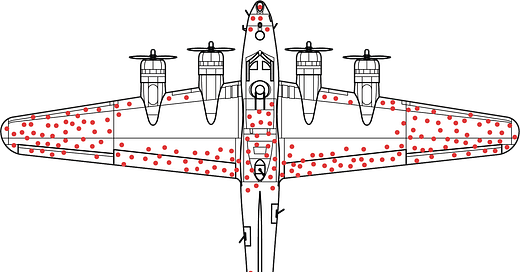
Since I was sticking it on merch, I didn’t want to just take the image that most people use when posting about it, the one from Wikipedia (below):
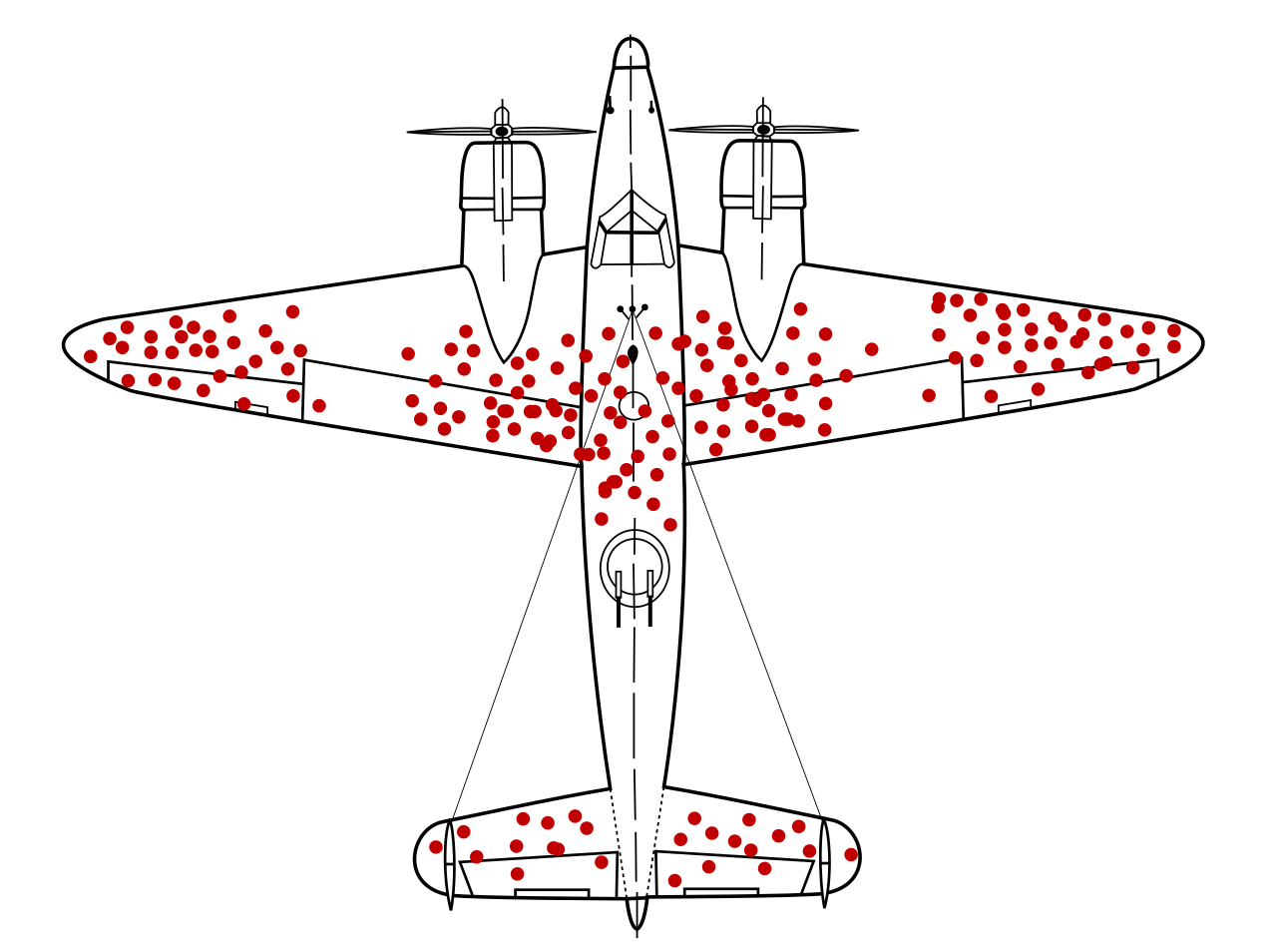
The Wikipedia version is based on a WW2 bomber, the PV-1 Ventura, while I based mine off the B-17 Flying Fortress. Both are WW2 planes because the story about how the diagram came into being traces to Abraham Wald during WW2, during which he did statistical analysis on damage that returning airplanes had. I just happen to like the B-17 more because it had a reputation for returning safely from bombing runs despite significant battle damage.
Only later, after I had put together the image by referencing other drawings, did I learn the amazing truth — Wald’s original work never had any diagrams in it.
I was lamenting about how I couldn’t find a source for the original diagrams, and got this tweet:

Which lit a flame in my curiosity on where the thing came from. (Thanks a ton for the tip and link to the original papers David!)
Once I knew to pay attention, I clicked the Wikipedia image to check where that version originally came from, and you can find this:
Illustration of hypothetical damage pattern on a WW2 bomber. Based on a not-illustrated report by Abraham Wald (1943), picture concept by Cameron Moll (2005, claimed on Twitter and credited by Mother Jones), new version by McGeddon based on a Lockheed PV-1 Ventura drawing (2016), vector file by Martin Grandjean (2021).
— Wikipedia survivorship bias plane image, emphasis added
Which seems to indicate that the mere concept of using a plane with bullet holes only came into being around 2005, and the beloved PV-1 version that gets memed across Twitter all the time came in 2016. I haven’t been able to come across any evidence to the contrary.
Well, since I sorta hit a dead end on this mystery trail pretty soon, and I have a stack of academic papers handed to me… the only reasonable thing would be to check out what’s in the papers? Right?
So what did Wald actually do back in 1943?
During the war, Wald was part of the Statistical Research Group of Columbia University. While there, the military would consult with the group for various questions, and Wald wound up with the question about developing a way to estimate plane vulnerability based on the damage observed on returning planes. Wald wrote eight memoranda about the topic, and in 1980, many years after the war, the memos that he had written were dug out of a box and published. You can find a copy here. It is almost 100 pages worth of equations and statistical reasoning.
The whole set consists of a eight parts, of which only one — number 5 — discusses the vulnerability of planes to hits on different parts. Most of the initial setup and derivations is analyzing the problem of estimating the probability of a plane going down after exactly i hits, anywhere on the plane, based on the data from surviving planes. It’s only until much later does any consideration of location happens, and that part only goes so far as to break the plane down into systems (fuel, engines, fuselage, and everything else), and only by estimating the percentage of area of the plane each part covers.
Since that statistical text is very dense, and the story of Wald and the airplane diagram is famous internet lore, Bell Casselman published a column in the American Mathematical Society about the legend behind the story of Wald and survivorship bias. Bill’s conclusion is that the specific tale told on the internet at large is likely apocryphal, but there are plenty of nuggets of truth behind it all. The column also tries to explain the core equation and reasoning that went into the original work.
But fear not! Despite the original memos having no diagrams and illustrations at all, and the very common disappointment when we hear that a famous bit of internet lore turns out to be an exaggeration, there is some mention that Wald actually did suggest that planes should have the armor increased in the places that didn’t return with bullet holes:
“The military was inclined to provide protection for those parts that on returning planes showed the most hits. Wald assumed, on good evidence, that hits in combat were uniformly distributed over the planes. It follows that hits on the more vulnerable parts were less likely to be found on returning planes than hits on the less vulnerable parts, since planes receiving hits on the more vulnerable parts were less likely to return to provide data. From these premises, he devised methods for estimating vulnerability of various parts."
— Postscript of Bill Casselman’s column
Poking at some of the math in the papers
Imagine if your boss came up to you and asked you this: “Hey, we have data on the number of warplanes that return with bullet holes in them. Can you give us a method for estimating what are the chances that a given bullet hitting a plane causes it to crash?”
I know what my reaction would be — *deer in headlights look*. So I wanted to see how that problem was solved.
Let’s be clear here. I’m not a mathematician by any definition of the word, and can’t prove myself out of a Pythagorean theorem. Reading statistical papers is also something I’ve actually never had to do in my life before this point. So I’m doing my best to summarize the highlights from secondary sources. If you’d rather not see someone bumble around at an unfamiliar thing, go check out the linked sources directly.
The column by Bill Casselman mentioned above describes a derivation central to Wald’s work, which would allow him to later derive bounds on the probability that a plane getting it an i-th time would go down or not.
At the same time, I’m also relying on Mangel & Samaniego’s (1981) “Abraham Wald’s Work on Aircraft Survivability” which explains much of the work more systematically, not only retracing Wald’s original line of reasoning, but also translating things into aa more modern statistical lens, though admittedly in terms that are still very dense to be my untrained eyes. If you’re good with multinomial models and MLEs you might find their more modern treatment easier to digest.
The setup
So the data Wald had available to analyze was relatively limited. Plus, getting more data involved waiting for more planes to go out and get shot down, or (I assume) very costly experiments involving real planes, guns and dummy bullets?
Number of airplanes sent on a mission
Number of airplanes that returned (thus, you know the # of planes lost)
Of the airplanes that returned, how many bullet holes the plane had and the location of the hole
Most importantly, we don’t know anything about the planes that were lost. They could’ve been hit by 1 bullet, or a million, or crashed due to random engine failure or pilot error. Also, in the 1940s, “computer” was the title for women hired to literally compute numbers and solutions to formulae manually, so you can’t just brute force some kind of iterative solution to everything.
Thus, the strategy available to Wald was to write out formulas to describe what is happening, write out assumptions that would allow his work to proceed further, then proceed analytically until he could find a way to manually calculate the values he was looking for.
Wald made some simplifying assumptions from the start. All planes were lost due to bullet strikes, as in, planes that aren’t hit all return. Also, there’s some maximum number of bullets that will hit a plane, after which the probability of getting hit more goes to zero (thus ruling out infinite bullet and similar unlikely scenarios). Wald capped the max possible number of hits at the maximum number of bullet strikes observed on surviving planes + 1.
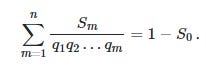
Bill’s column explains the derivation of that core formula, which makes use of the fact that there’s that cap on the max number of bullet hits, and assumes a universe where only dummy bullets are used. The formula is important because it allows you to relate the number of surviving planes with various bullet hits (a value we have) with a product of a bunch of probabilities of surviving the i-th bullet strike (all the q values in the denominator).
Normally this feels like a dead end because we still don’t have a way to derive the values of q with our data. While we’d normally expect bullets to weaken a plane and increase it’s chance of failing, we could also simplify things by assuming bullets all have equal effect, all q values are the same. This would reduce the above formula to be:
To my understanding, the dummy bullets assumption is required because it allows you to define the ideal scenario where all planes return and allows you to draw the red line in the graph, y = 1-a_0 (the assumption seems to provide the critical 1 in the equation). You could then solve for q in this scenario by filling in all the values for s, the proportion of surviving planes observed with n bullet holes and get an analytical result based on your data.
The blue line in the above graph is just the other side of the equation, and the solution is where the two curves cross. Just fill in your values for a_n from your data, solve for q up to the maximum number of bullet strikes you assume are possible, and solve for q.
The only problem is that this result only holds true for when all values of q are equal. In reality, we all have the intuition that getting hit with more bullets should increase the chances of a plane to go down, not just have equal chance as all bullets before it. So much of Wald’s continued work would be to try to relax that assumption via various strategies.
The problem with finding an exact solution to the problem is that it requires a lot of calculation power that wasn’t available in 1940. The solution requires solving a nonlinear optimization problem for every unique unique array of q_n variables. The steps needed to arrive at the solution is similar each time using a Lagrange multipler method, but the details change every time. Since you need one q variable for every bullet assumed to hit the plane, it gets really messy.
Instead Wald needed an approximation to set the bounds for the probability of a plane going down when hit by the i-th bullet. To do this, he makes some more assumptions that allow him to do some algebraic rewrites and come up with bounds. It’s at this point where my tenuous ability to follow the math goes way out the window. Check out page 5 if you’re interested and up for a challenge.
The section later on about looking at the different parts of aircraft getting struck and the effects thereof involved breaking the plane up into different sections — here it was fuel system, fuselage, engines, everything else. The math actually allows you to divide the plane up into as many parts, k, as you’d like.
Then you could either empirically measure how often each section was hit (with a plane and dummy bullets), or use the percentage area of each part as a stand in, thereby assuming bullets are uniformly distributed. While there’s a lot of formula derivations and algebraic rewrites in the analysis, eventually Wald invokes an assumption of independence over where bullets hit. Any part of the plane getting hit and surviving does not depend on any part getting hit at any time prior. It allows him to not have to deal with conditional probabilities on where bullets land and allows him to find an analytical solution to the problem.
Okay okay I’m done!
As this being the first academic statistics paper I’ve ever read in any context… this had been a heck of a learning experience. Mostly of the “I do not have the short-term memory muscle to juggle arbitrary math symbol definitions” kind.
Thanks for humoring me in my curiosity!
Hey, wait up, didn’t you say something about enamel pins?
Uh, yes. I’m looking into it.
I’ve got a candidate design for a 1-inch pin, but I need to see if it’s actually manufacturable. The main roadblock is locating a factory that makes them, getting a batch manufactured, then shipped to me where I then have to figure out the logistics of selling and shipping the tiny things. That’s a lot of work for an already hectic holiday season.
So I’ll chip away at it between other things going on. Maybe by 2022?
Until then, there’s still the shirts, which I hope people like.
About this newsletter
I’m Randy Au, currently a Quantitative UX researcher, former data analyst, and general-purpose data and tech nerd. The Counting Stuff newsletter is a weekly data/tech blog about the less-than-sexy aspects about data science, UX research and tech. With occasional excursions into other fun topics.
All photos/drawings used are taken/created by Randy unless otherwise noted.
Curated archive of evergreen posts can be found at randyau.com
Supporting this newsletter:
This newsletter is free, share it with your friends without guilt! But if you like the content and want to send some love, here’s some options:
Tweet me - Comments and questions are always welcome, they often inspire new posts
A small one-time donation at Ko-fi - Thanks to everyone who’s supported me!!! <3