Given the state of the pandemic and rapidly developing war going on, I hope everyone out there is as safe as can be.
This weekend, I had to drive the family around for various errands, and as I followed the satnav system on my phone, I started wondering about GPS. But this post today is not going to be a discussion about GPS — we’ll leave all the fun stuff about flying atomic clocks in space for another day. Instead, I was thinking more about more fundamental stuff — how do we translate a GPS coordinate, which is this arbitrary 4-dimensional point in spacetime, into “a place on the planet Earth”? What goes into that?
We’re going to be essentially working backwards from GPS to ultimately measuring the shape of the Earth. Historically this is reverse from how things were actually invented and developed.
Problem setup
While I’m not going into the details of how GPS functions, I’ll zoom over the basic ideas to set up the problem I’m talking about.
At it’s core, satellite navigation systems is a constellation of satellites (in the case of GPS, there’s 24 active ones out of 31 functional in orbit) that broadcast their exact time and location. Receivers use the information from usually 4 or more satellites to calculate their location on the Earth’s surface.
The receiver can figure out the position because every satellite’s time+location draws a sphere around the satellite because the speed of light is constant. There are only 2 points in the universe that hears the unique set of 3 timestamps heard by the receiver, and typically only one of those two points is on the Earth’s surface. The diagram below shows the two points, A and B, that satisfy the conditions. This particular problem is called true-range multilateration.
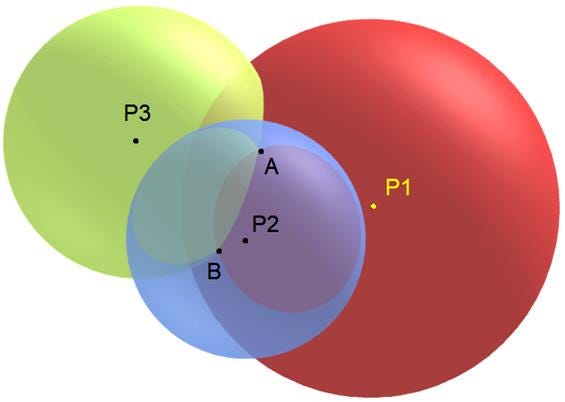
The question I want to cover today is, what do GPS devices like our phones use to convert this arbitrary abstract point in an arbitrary coordinate system, A, into a “place” that we recognize, like a latitude/longitude/altitude coordinate. How does any of that work?
Today I want to explore a bit of the world of Geodesy, the study of measuring the Earth’s shape, size, orientation in space and gravity.
Hopefully this isn’t a completely foreign topic to you all by now because we’ve actually touched upon the “orientation in space” part before when discussing potential negative leap seconds and the rotation of the Earth.
Geoids, Ellipsoids, and Gravity maps!
Returning to GPS, the way that GPS connects to the real world is through a standard called the World Geodetic System (WGS). It specifically uses the WGS84 standard that was initially published in 1984 (and has been continually updated since). The standard provides us the coordinate system that we use, as well as a bunch of other complex models of the Earth.
As an example, the Empire State Building is located, according to GPS, at 40.7484° N, 73.9857° W. It’s important to note that the Empire State Building only has that location based on the WGS84 coordinate system. Someone could easily define a coordinate system that uses the building as the 0,0 origin point or any other numbers. Coordinate systems are completely arbitrary constructs that we define for convenience.
WGS84 places the origin of the coordinate system at the center of mass for the Earth. Mass is important here because the Earth isn’t uniform in shape or density, so some kind of geometric center would be a different point. Satellites also orbit around the center of mass, so it makes for a natural origin point.
WGS84 uses the same prime meridian as the IERS Reference Median. This is effectively the Royal Observatory at Greenwich, and is maintained by the folk at IERS who, among other things, are the people who determine when a leap second is declared.
Along with the prime meridian, WGS84 also gives the parameters for the oblate spheroid with equatorial radius a = 6378137 m at the equator and flattening f = 1/298.257223563. There’s many other parameters in the definition that aren’t really important for us to know — ultimately it just defines this smooth mathematical object upon which all our maps, objects, distance calculations, etc. can be projected upon.
There are other coordinate systems (called geodetic datum, such as the North American Datum, ETRS89 for Europe) that are in use by various other people/groups for various reasons. Also note that the datum I’ve mentioned so far are horizontal datum, they define what we consider the horizontal coordinate system along the surface of the Earth. There are also vertical datum which we’ll get to into now.
So, what’s up with “up”?
Think back for a second about the oblate spheroid coordinate system that GPS uses via WGS84. Notice how it has a specific radius in meters, and then constants tweaking its specific shape, but is otherwise just a smooth mathematical object that’s be (somehow) tuned to represent the shape of the Earth. How is vertical altitude represented? While you can (and we do) calculate how far above/below the reference ellipsoid that defines latitude and longitude, how closely does that relate to the real world altitude?
Explaining this takes a bit of a detour.
Before the age of satellites, hyper accurate GPS measurements and WGS84, how would people define altitude? Probably the easiest answer is “use the sea as 0” — and that’s what people did. They used a concept called the “mean sea level” which accounts for high and low tide. You’d drop a weighted plumb line, it gets pulled straight down by gravity, reference it to the mean sea level, and you now have altitude measurements. The assumption was that the sea (if the tides and waves were ignored) represented a universal height at equilibrium with gravity and was the only true reference point.
But the world isn’t nearly that simple. What scientists eventually discovered was that due to the uneven density of the Earth, gravity isn’t evenly distributed. There are places that are less dense and thus have sliiiiiightly less gravity than other places, just like there are places that are more dense and thus have slightly more gravity.
The implications of these slight differences in gravity is actually very interesting. Water actually flows from places with less gravity to places with more. So if the Earth was completely covered with enough water to cover the tallest mountains, with no atmosphere for wind nor currents, the water would actually form high and low spots according to gravity. It would not become a perfect ball unless the density of the Earth is also perfect. There’s actually no single “mean sea level” that applies globally, it’s a local phenomenon.
The concept I’ve been describing here is called the “geoid”, it’s very lumpy description of the gravity of the Earth that’s now measured by extremely sensitive satellites orbiting overhead. Scientists picked a line of equal geopotential (the sum of gravitational potential energy and centrifugal potential energy) to define a surface that largely agrees with Mean Sea Level. From my understanding, every point on the geoid’s surface is perpendicular to the plumb line at that point, because local gravity anomalies will deflect the plumb line to a side.
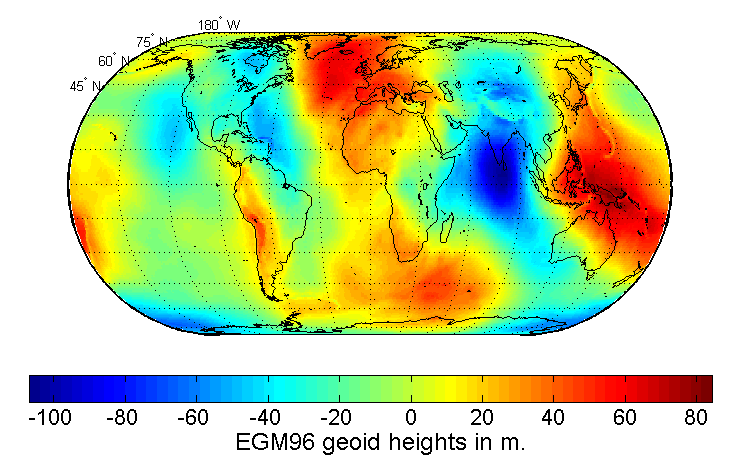
This geoid, and its relationship to the plumb line, gives us an absolute 0 point to use as a reference for our height measurements. The problem is that there is no magical mathematical description of the geoid. It is completely defined by the Earth, and can even change over time due to plate tectonics and the flow of material in the Earth’s mantle.
While the WGS84’s model was built to try to approximate mean sea level, you can’t fit a smooth globally defined curve to a completely arbitrary and bumpy gravity map perfectly. Thus WGS84 and the geoid disagree and GPS equipment that needs to report height in ways that we expect, has to use a lookup table to convert the GPS ellipsoid height, to one based upon the geoid and MSL.
Circling back to our daily lives
So this brings me to the end of this week’s wild foray into learning about the coordinate system that we all take for granted. There’s a bunch of other details that I haven’t managed to dig into yet, for example WGS84 also includes a model for the earth’s magnetic field (World Magnetic Model), and I have no idea how it’s used.
But now, at least we have a rough understanding of why is it that scientists could say that the main island of Japan had moved 2.6 meters eastward after the huge 2011 Tohoku Earthquake.
References and cool stuff I found along this journey
A SUPER awesomely thorough and friendly explanation of GPS that @mgilbir linked me to. It goes right down to the actual GPS message transmissions. I’ll be referencing it a ton when/if I go down a GPS rabbit hole.
Probably the most useful resources I’ve found online to help understand much of these concepts come from reference material for GIS software. For example, ESRI had lots of explanation of things like the geoid and MSL
There was a really cool space mission by the ESA called GOCE that sent a satellite up from 2009-2013 that orbited the planet at low altitude (for a satellite), used an ion engine to negate the effect of atmospheric drag, and produced the most detailed gravity maps of Earth ever. It was also used to study ocean currents because the difference in density is detectible via gravity. It also detected echoes of Japan’s 2011 Earthquake, accidentally becoming the first seismograph in space. On to of other research, the detailed data from the satellite was used to update the geoid.
Data community stuff I’d like to share
@_eigenfoo also would like data scientists to collect more data, listing out many benefits of learning to do so.
Standing offer: If you created something and would like me to review or share it w/ the data community — my mailbox and Twitter DMs are open.
About this newsletter
I’m Randy Au, currently a Quantitative UX researcher, former data analyst, and general-purpose data and tech nerd. Counting Stuff is a weekly data/tech newsletter about the less-than-sexy aspects about data science, UX research and tech. With excursions into other fun topics.
All photos/drawings used are taken/created by Randy unless otherwise noted.
Curated archive of evergreen posts can be found at randyau.com
Supporting this newsletter:
This newsletter is free, share it with your friends without guilt! But if you like the content and want to send some love, here’s some options:
Tweet me - Comments and questions are always welcome, they often inspire new posts
A small one-time donation at Ko-fi - Thanks to everyone who’s sent a small donation! I read every single note!
If shirts and swag are more your style there’s some here - There’s a plane w/ dots shirt available!




It's even stranger. NAD83, the North American Datum is tied to the North American plate. In the 80's, NAD83 and WGS84 were essentially identical - differed by millimeters. Now they are several feet apart as the North American plate moves about 1 cm per year.
Many years ago (early 80's) I taught a short class in geodetics, and a geodecist I worked with made a viewgraph for me showing how a particular well offshore Angola would move by up to a kilometer depending on which geodetic datum you attached its lat-long to. There are many local datums, designed to better approximate local topography. I spent a lot of effort teaching people that knowing the lat-long of a point did NOT tell you where it was on the earth. You also needed to know the datum.