This past week has been an unbelievably hot week on planet Earth. A heat dome over the Pacific Northwest set record temperatures and the 115F record temperature contributed to massive wildfires in Canada, Antarctica set a new high temperature record of 18.3C, and the Gulf of Mexico caught on fire (okay, that was a gas line explosion). New York City, where I am, only experienced a minor heat wave just a few degrees shy of 100F.
So in all this heat, I kept thinking about the curious unit that is reported in the US whenever it gets hot — the Heat Index. Depending on where you get your weather information, it is sometimes reported as a trademarked thing, a “Feels Like” temperature. As a data person and philosophy student, I’ve always been confused by the unit because how can you say “In this 95F + humidity/etc conditions, it feels like 105F”? How can anyone know how I would feel in 105F weather compared to anyone else? That’s essentially Wittgenstein’s beetles in a box thought experiment for the private language argument. There’s no guarantee that what I’m experiencing as “105F weather” is qualitatively the same as anyone else’s experience. The “Color Blue” I experience might not resemble in any way the “Blue” that you experience, but due to how language works, we all agree that those experiences are labeled “Blue”.
So I’ve always wondered what the heck Heat Index was about (and it’s related sibling unit, wind chill). I had already heard somewhere that measurements of wind chill derived from experiments of exposing people to cold, windy conditions in wind tunnels and seeing how they reacted, which is pretty much as sketchy as it sounds. Is heat index defined as weirdly?
This week’s article is a dive into the history and science that went into such a measure.
I should note here that Head Index is not a universal concept. Canada uses a similar but dimensionless measure called “Humidex” which is based around temperature and the dew point instead of relative humidity.
A Washington post summary of the history of Heat Index from 2011, (which apparently was written because Rush Limbaugh had been spouting some nonsense about the measurement around that time) traces things back to the early 1900s, where Osborn Fort Hevener coined the term “Humiture” as a way to describe the relationship between temperature and relative humidity. A “humit” was defined as the temperature in (Fahrenheit + Relative Humidity percent)/ 2, essentially an average of the two numbers if you ignore the units. The thinking goes that the higher the humiture, the more uncomfortable a person would feel.
Over time, meteorologists take the concept progressively more seriously because there definitely is utility in expressing how uncomfortable certain combinations of temperature and humidity is. If those numbers gets past a certain point, it can get downright deadly.
So Steadman in 1979, publishes The Assessment of Sultriness, Part I and Part II to formalize a model for “sultriness” that we use to this day as the basis for the modern definition of Heat Index. By the time Steadman publishes his paper, the concept of having an apparent temperature scale tuned to human physiology has been bounced around already in the literature (he cites various papers that come to such a conclusion). Steadman’s contribution was laying out/choosing the very many parameters that must go into such a model to get a relatively objective function that calculates the apparent temperature.
What goes into defining the Heat Index
Steadman’s approach to defining (what would become) the Heat Index is largely a thermodynamic one. At a high level, the reasoning for Heat Index goes like this:
the human body generates heat that must be dissipated
we dissipate heat mostly via radiation, convection, and evaporation
local conditions make dissipating heat harder by resisting heat transfer in any of the heat dissipation methods, humans sweat and/or remove clothing to compensate until we hit thermal equilibrium
that resistance to heat dissipation is a complex function we’re going to model
equivalent dissipation resistance “feels the same” in terms of sultriness
that feeling of sultriness at a reference humidity level gives us the Apparent Temperature, aka Heat Index.
The majority of the paper then goes into all the parameters (and models for those parameters) that make up the calculation for how much heat and moisture a human is transferring out into the environment. Here’s the (mind-blowingly long) list of factors considered and assumptions that go into them.
“Mild” vs “Severe” sultriness — Mild is defined as temperatures within 20C-25C and Severe is from 26C to 50C. The model is non-linear and the assumed model parameters can differ between the two conditions.
Typical meteorological conditions — the model is tuned for conditions typically found on Earth (and more specifically, North America). It’s not designed to handle temperatures, barometric pressures, etc. outside of what is considered possible. No 5000 Kelvin temperatures nor near-vacuum pressures.
Size of a “typical” human — assumed to be 1.7m and 67kg regardless of sex. That human is assumed (w/ data from other studies) to have a surface area of 1.78 m^2.
How much skin area can exchange radiant heat — expressed as a ratio of radiant area/total surface area. Assumed to average 0.79 for clothed body parts, 0.95 for bare body parts. Under severe conditions where the human would wear no significant clothing it’s assumed to be 0.80.
The “Significant diameter” of a human — a unit apparently used in convective heat transfer equations, defined as 4(volume)/(surface area) of a human. Given the assumptions used, it is 15.3cm.
Clothing cover — assumed to be 84% (long trousers and short-sleeved shirt/blouse). But can be 0% under severe conditions. Apparently a bare 5mm thickness worth of clothing (air gaps included) for modesty does not seem to affect the sultriness model much.
Human core temperatures — while some humans (like athletes) can have higher core temperatures while exerting, the paper generally assumes that humans want to maintain a 37C core temp, and everything is calculated with that target core temp in mind.
Human core vapor pressure — How much water in the body wants to evaporate and leave (this doesn’t affect sweat on the skin, but things like lungs). Based on prior studies and assumed to be 5.65kPa.
Surface temperature and vapor pressure of the skin — needed because these parameters affect how much heat the skin is transferring to the environment. It’s a calculated parameter based on taking the core temp/vapor pressure and bringing it to equilibrium with the external temperature and vapor pressure via an iterative process.
Activity level — Needed since the Heat Index is trying to balance heat generated by the body against heat being transferred to the environment, and activity increases heat generated by the body. It’s assumed to be a human walking at 1.4m/s (~3mph). It corresponds to 180 watts of power per square meter of human surface area.
Effective wind speed — since even a very slight breeze can make a different in how much heat a human can transfer to the environment. Assumed to be 5 knots (~2.5m/s) worth of wind, barely detectable by an anemometer. Since the assumed human is also walking 1.4m/s and can be walking at any angle to the wind the average speed between the two is calculated and used.
Ventilation rate — because breathing out transfers heat and water through the lungs. Assumed to be 2-12% of a person’s total heat loss (the 180 watts from activity), depending on the relative humidity level
Skin’s resistance to heat transfer — effectively the difference between the body’s core vapor pressure and the skin’s vapor pressure over the surface area of the skin. 0.0521 m^2*kPA/W
Clothing resistance to heat transfer — modeled and assumed to be summer clothing of 20% fabric, 80% trapped air
Clothing resistance to moisture transfer — assumed to only be the vapor diffusion through the fabric, requires modeling how vapor diffuses through the layers of clothing
Surface radiation — a coefficient for how much heat is radiated by the body and clothing based on body temperature vs air temp
Surface convection — calculated using the Significant Diameter from above and the assumed 5 knots wind speed, averaged over all possible angles of the wind.
How skin resistances to heat and moisture transfer are related — because as sweating changes how the skin resists moisture transfer, and vasodilation changes how skin transfers heat, the value of one is modeled against the other.
Other assumptions — Everything is in a steady state (no wind gusts). The human is capable of sweating enough to achieve thermodynamic equilibrium at an apparent temperature of 50C, etc…
PHEW.
Now all that remains to be done is to calculate the amount of heat transferred from the clothed and unclothed parts of the body to the environment for a given air temperature and relative humidity. Steadman derives a series of equations based on the heat loss from clothed and unclothed parts of the body. Finally, everything is converted into a resistance to heat transfer from the body, meaning the clothing we wear, the ambient weather conditions, are all working to make it harder (or easier) for our bodies to dissipate our generated body heat. Effectively, that effort needed to overcome the resistance is the cause of how we feel uncomfortable in sultry conditions.
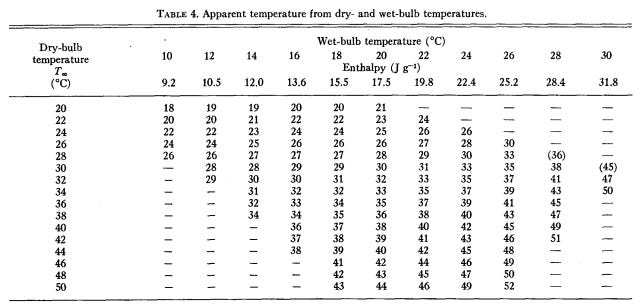
After a ton of algebra and equation juggling later, you can take any temperature/vapor pressure pair, and solve for the equivalent temperature if the vapor pressure of the environment is 1.6kPa (the assumed standard “normal”). That solution is the apparent temperature and our Heat Index. Due to the overwhelming complexity of the model, Steadman calculates tables for us where if you know the certain parameters, like dry bulb, wet bulb temperatures of a sling psychrometer, the dew point, or relative humidity, you can get an apparent temperature.
BUT WAIT! There’s more!!
If I haven’t overloaded your short term memory with roughly 19 model parameters already, you might have noticed the model is essentially talking about a human walking in a breeze of 5 knots under various temperatures and humidity values. Essentially, the human is sorta walking in an idealized shady wind tunnel. What if the sun is shining or the wind is blowing? What if we’re on top of a mountain?
Handling these new conditions is the basis for Part II of Steadman’s papers, and he notes that there are 3 major sources of environmental factors that could have an effect on apparent temperature: wind, extra radiation, and air pressure.
Wind is interesting because how it affects our bodies depends not just on the wind speed, but also on the ambient conditions — a wind lower than body temperature often helps to cool us, but higher than body temperature can actually heat us up. One interesting note from the paper is that under full direct sunlight, wind almost always has a cooling effect thanks to how it helps with evaporation. It’s under shade that the situation can vary.
Extra radiation factors in extra heat coming from the environment that wasn’t modeled originally. Obviously there’s the heating effect of direct sunlight, as well as heat radiation bouncing off objects in the environment, but also there’s heat radiating from the earth itself (for example hot sidewalks) as the sky itself radiates a small amount of heat radiation. All that winds up putting more heat into our bodies that needs to be dissipated out, which can be hampered by the humidity.
Finally air pressure effects means altitude, because that’s the biggest driver of air pressure differences experienced by humans. Air pressure does two things: it makes convection more difficult because the air density drops and moisture transfer is harder, but heat loss from exhaling increases (both due to increased breathing volume due to altitude and the lower vapor pressure). Thankfully, the forces wind up balancing out to within about 0.5 degrees difference when calculated and therefore can be omitted. Phew!
This is way too much, why can’t there be one formula instead of a nest of models?
You’re not the only person to have asked this exact question. The model calculated by Steadman is pretty thorough and full of reasonable assumptions, but it takes a lot of work to calculate since some of the calculations require iterative processes to home in on a steady equilibrium state. I’m sure that modern computers can do the calculations in seconds, but even then it’s pretty awkward.
So instead, people like Rothfusz in 1990 published a simpler approximations of the original Heat Index model. The typical method is to use everyone’s favorite tool, curve fitting via multiple regression, to approximate the curve of the outputs of the full model, using only temperature and relative humidity as input variables. Rothfusz’s formula, which is used by the National Weather Service for US forecasts, is supposed to have an error of +/- 1.3F versus the true Heat Index.
But due to the complexity of the HI model, guess what, it has adjustment values tacked on in certain conditions to help keep it in within acceptable error despite the non-linearity. To save on space, I’ll screenshot the NWS’s equation that’s been put out by Rothfusz:

What’s all this mean for us mere mortals?
First, Heat Index is “real” in that while it makes quite a lot of assumptions, it does come to a fairly objective determination for why one temperature/relative humidity condition “feels like” another.
Next, the assumptions are for a very particular human of 1.7m height an 67kg, walking, in a 5 knot wind, without the sun shining on them. Deviations from those parameters will mean the Heat Index for you will be very slightly different, but the error tends to be low.
Probably the biggest exception is when it comes to being in direct sunlight, because that sun puts out a ton of heat that we’d be forced to dissipate in already difficult conditions. Part II mentions that direct insolation can add as much as 7.5C to the apparent temperature. Stay out of the sun.
Exertion is also a bad idea because anything over a steady walk is out of the assumptions in a negative way.
What’s also very impressive about the context is that all the assumptions and parameters that went into the model had to come from prior studies on a whole range of topics. Things like how does clothing impede water vapor transfer, what the surface area of a human is, how we expel heat through our lungs, etc.
Finally, EVERYTHING I can find that uses Heat Index uses the NWS Heat Index equation. I haven’t been able to find any code, in any language, that re-implements the complicated series of calculations that Steadman uses. Which would have been really fascinating to have now because we could use the cheap and plentiful computational power available to calculate personalized heat index values, according to whatever parameters we choose, including making ones for exertion due to activity and current wind speeds.
I suspect that the “branded” versions of the Heat Index in use by various weather reporting companies actually have reimplemented their own version of the Steadman equations, making changes to any assumptions that they feel is more relevant, including possibly adding in parameters to handle sunlight or predicted wind speeds.
So there you have it, a long look into just how complicated the physical system of humans dissipating heat into the environment just so we don’t cook ourselves with our metabolism.
Stay cool out there in the summer!
About this newsletter
I’m Randy Au, currently a Quantitative UX researcher, former data analyst, and general-purpose data and tech nerd. The Counting Stuff newsletter is a weekly data/tech blog about the less-than-sexy aspects about data science, UX research and tech. With occasional excursions into other fun topics.
All photos/drawings used are taken/created by Randy unless otherwise noted.
Supporting this newsletter:
This newsletter is free, share it with your friends without guilt! But if you like the content and want to send some love, here’s some options:
Tweet me - Comments and questions are always welcome, they often inspire new posts
A small one-time donation at Ko-fi - Thanks to the folks who occasionally send a donation! I see the comments and read each one. I haven’t figured out a polite way of responding yet because distributed systems are hard. But it’s very appreciated!!!