Huzzah! The first long-form post in a while. Apologies to everyone who’s missed reading these, I missed writing them too. Summer’s a hard time to find space to do research when there’s a 3 year old zooming around between summer activities. If you have ideas for interesting topics you’d like to nerd snipe me with, particularly ways of measurement, interesting data sets, or fun technology, please let me know.
This post all started because some time ago, I stumbled upon a link to the National Geodetic Survey Explorer and kept the tab open for months before spotting some surveyors recently. This tool lets you search within the US and find the location of various kinds of survey markers. Guaranteed you have some near you right now. What are those? They’re physically marked points where the location is “known” because they’re part of larger efforts to locate things (more on this later). If you’ve ever bought property and ordered a survey done to get a detailed report of where the property lines are, those surveys typically rely on similar markers as initial reference points.
As an example, here’s the datasheet for a marker that’s the corner of the Sherman statue in the southeast corner for Central Park, NYC. If necessary, you could take measurements off that point to designate the locations of other stuff nearby. All these points are incorporated into a geodetic control network that tracks all this stuff.
These days, we now have hyper-accurate satellite systems that let us know the location of a point down to extreme precision — scientists can use such systems to figure out how much the earth’s crust moves over time. I wrote about GPS and the complex coordinate system called the geoid that represents the earth in a previous post. But the first GPS satellite was launched in 1973 and humans have been creating detailed maps of places long before that. How did we do it to any level of precision?
Today we’re going to dive into mostly 19th century efforts of measuring out entire countries. That era of measurement represents some of the largest efforts to measure entire countries prior to the development of satellite positioning systems that are used today.
To be clear, humans have been drawing maps and surveying land for millennia. Making large, accurate, layouts is a requirement for constructing large structures going as far as the Great Pyramids. There’s records of various civilizations using trigonometry to survey land for ages. But from the 1600s onwards, the methods and techniques for measurement became increasingly refined, and by the late 18th, early 19th centuries, rulers started funding the very detailed measurement of their domains. For example, Britain had one done starting in 1791, India’s started around 1801, the US did one starting in 1871. These “triangulation” survey projects were extremely labor intensive and took multiple decades. They predated the automobile, so people had to travel on foot, carriage and horseback carrying heavy survey equipment across the countryside and wilderness while taking detailed measurements.
Why’s were the projects called “triangulation”?
The basic idea behind these measurement surveys is fairly simple.
If you have a triangle and know two of the angles and the length of one of the sides, you can calculate all the lengths and angles of that triangle using trigonometric functions. Then, you can keep adding on more vertices and triangles to your existing measured triangle and propagate the original measured distance (the baseline) to the new sides. All you would have to do is measure the angles between the different vertices. You can build a whole network of triangles off this method. Do this on the scale of many miles and you have a way of measuring the distances of a large landmass. With the help of a technique called resectioning you can calculate the location of any point within the network.
What’s great about this triangulation method is that you theoretically only need to make one length measurement — the initial base-line, the critical one side of the first triangle. After that, you just have to go measure the angles between your triangle vertices. You could then calculate all the distances with trigonometry.
The Great Triangulation Survey of India
So how was one of these massive undertakings done in practice? How does one actually measure a country? To look at this, I’m going to reference the 70 year effort to triangulate the Indian subcontinent in 1801-1871, primarily because there are a lot of records and source material available documenting the process compared with other triangulation efforts.
I should also note that the whole project is deeply rooted in the imperialism of the era. It started off because the British East India Company had recently won a war in the southern peninsula and realized their maps weren’t accurate enough for their needs. They wanted a better accounting of the territory they controlled, as well as descriptions of what was on it.
The project then went on through the decades, through famine, drought, conquest, armed revolt, and even past the end of the British East India Company’s rule (where the British government took over) in 1858 before completing in 1871. I don’t know the history of the time well enough to even have the slightest sense of what happened, but it was definitely not a peaceful one.
For the most part I’ll be referring to the earlier efforts prior to 1830, much of which is documented in the Account of the Operations of the Great Trigonometrical Survey of India, volume 1. It’s available as a big scan on Google Books since it’s in the public domain now.
The whole endeavor is quite famous due to its scale, as well as its scientific contributions. It was one of the first attempts at measuring the length of a section of longitudinal arc (known as the “Great Arc”). It was also the project that measured the heights of some of the tallest mountains in the Himalayas: Everest, K2, and Kanchenjunga. Mount Everest itself was named after George Everest, the surveyor who measured the Great Arc and later led the Great Trigonometric Survey (despite the objections of George Everest himself).
The measurement of the arc was also the first time scientists noticed that some measured distances were off due to how local gravity affected plumb lines, a phenomenon known as geodesic anomaly. That notion would eventually help define what “sea level” means in our modern conception of measuring the earth.
Along the way, since the project took so long, methods, technology, and even the people doing the work, changed during over time. Halfway through in 1830, the accuracy of the old base-line length measurements were called into doubt and effectively replaced.
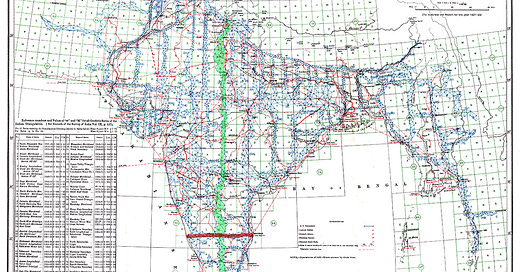
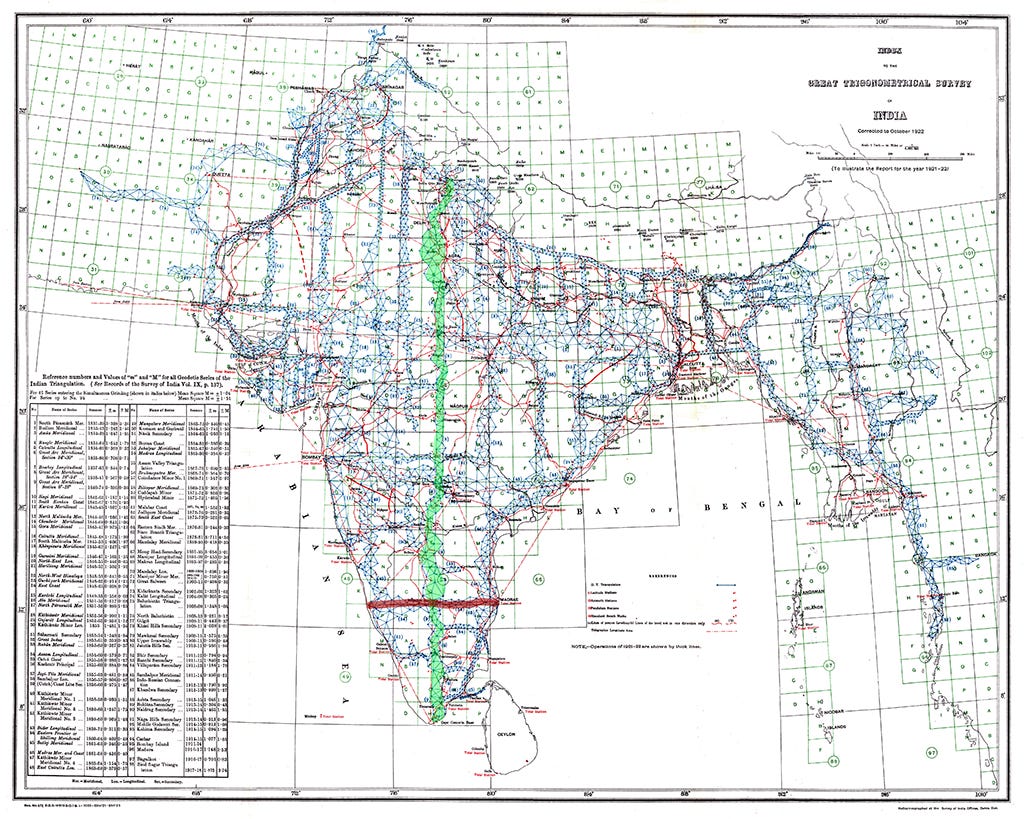
Despite the change in implementation details, the general strategy of the triangulation survey remained the same. They would measure the land along various longitudes (“meridians”) and latitudes to make up a grid that described the landmass. The land was far too large to cover entirely with the survey, so if you look at the map at the start of this post, you’ll see in addition to the network of bluish triangles following longitude/latitude lines, they focused their measurements along the coastlines, borders, and major rivers.
Highlighted in green is what is referred to as “The Great Arc”, which was a primary measurement goal in the early days because no one’s measured a large section of longitude before. It roughly split the land into two halves, and represented much of the north-south length of the territory. A red highlight towards the southern tip marked the original triangulation attempt made by Lambton before the project spread to the entire Indian subcontinent.
Figuring out Latitude
Of all the data points they needed to collect to locate a point, latitude was the most straightforward — use the stars. The problem is doing so with enough precision for this mapping endeavor. The solution used was to use a Zenith Sector, which is a mostly vertical telescope with very fine angle measurements that you point at a star with a known angle from Polaris.
Interestingly enough there’s no mention of measuring longitude precisely in the records. It might be because it’s not necessary since they’d be marking out distances and you can figure out longitude that way. There also isn’t any mention of them taking chronometers with them to measure longitude directly.
Measuring out the base-lines
One of the most important tasks for doing a triangulation survey that will stretch thousands of kilometers (modern India is very roughly 3,000km in extent when measured both from north-south and east-west extremes) is having a highly accurate starting length measurement for your initial triangle. It will the only length measurement that is made, and any error in measurement, however tiny, will propagate and throughout the rest of the triangulation network. So extreme care was taken to make sure the measurement was done as accurately as possible.
Measurement of this length was done using a 100 foot chain made of steel that had been referenced against length standards in England before being shipped over to India.
But having a standard-length chain wasn’t enough, you can’t just throw it on the ground and flip it end to end and expect an accurate measurement (plus the wear on the chain would eventually mess with the measurement). Here’s the bit describing the original method of using the chain used prior to 1830:
To summarize the long description, they would drive 3-inch diameter iron-bound stakes into the ground to a height of three or four feet. Those stakes would support 20-foot long planks called “coffers” that were 7 inches thick and 6 inches wide. These coffers would support the length of the chain. There would be a screw adjustment that allowed the chain ends to be slid with fine precision to where it needed to be. Finally the far end of the chain would have a pully that suspended a “8 1/2 inch shell” to keep constant tension on the whole chain.
Five thermometers were then set into the coffers for a period with a cloth covering them before their readings were averaged to allow for thermal expansion of the chains to be compensated for later. As evidenced by sketches of the process, tents were also erected over the whole setup to shield the chain from the thermal effects of the sun.
The whole setup was also considered to be measuring the hypotenuse of a right triangle, and they’d presumably use a plumb line to determine their angle away from true horizontal and adjust their measurements accordingly. This process would lead them to find those geodesic anomalies where the plumb line would be slightly off due to things like iron deposits in a nearby hill.

As you can see, accurate measurement of the base-line was a Big Frickin’ Deal. The original baseline in 1802 measured slightly over 40,000 feet in length, so this process would have been done over 400 times to cover a mere 7.5 miles of length.
Moreover, as technology progressed, these baselines taken prior to 1830 had various measurement issues raised, such as whether the chains had really been based off the standard lengths claimed. Some of the base-lines even stopped using coffers because of the time and labor involved and had laid the chain down on leveled and cleared ground. This was all judged to have added unacceptable errors and those base-line measurements were later superseded by even more accurate methods later.
Later, an apparatus invented by Colby called compensation bars — you had a pair of ten foot iron and brass bars rigidly attached at the center but allowed to thermally expand at the ends. The two ends were joined with a pivoting indicator while still allowing both bars to thermally expand freely. The location of the pivot points on the bars are placed according to the ratio of the thermal expansion coefficients of the two bars. The end result is that if both bars are exactly the same temperature, the indicators will always point to the exact same length, no temperature correction of the chain is needed.
Microscopes (!!) were then used to align and level the ends of these compensation bars. If the land was relatively flat, they’d essentially move the setup horizontally, leveling the ground as needed. On more significant slopes, they’d use trigonometry to figure out the true horizontal distance measured.
Note: the records state that measurements every 90-250 miles would be verified through the measurement of a base-line (page xxvi). So while theoretically, only one base-line is ever needed, in practice a LOT MORE were actually measured to provide verification checks.
Measuring out angles
While measuring base-lines was this extremely labor-intensive process, they all took less than a year to complete because they would only cover a number of miles. What would take up the remaining decades would be measuring out all the points on the triangles needed to extend the length measurements up and down the whole subcontinent.
The critical measurement of angles was done by a tool called a “theodolite”. The basic idea is that these are spotting scopes that are attached to multiple measurement wheels so that you can spot two points and measure the both the horizontal and vertical angle between them. Again, since these angle measurements will be the only thing that determine most of the lengths in the whole project, they need to be measured with extreme precision. The original theodolite used by Lambton for the survey of India was called “The Great Theodolite” and noted to be a “three-footer” (I assume it refers to the diameter of the base measuring wheel). You can see a picture of it at Getty Images, it is taller than a soldier and twice as wide! That particular model, being an earlier device, likely weighed around 200 pounds (990kg).
This theodolite would need to be carried to observation points, on top of mountains, hills, towers, whatever it took, so that the surveyors could sight the other points in the triangulation network. I’ve seen some mention that the theodolites weren’t transported on wagons/carts either due to lack of roads — the components would be be carried on poles by teams of men and reassembled on site.
On one occasion a rope snapped while they were hoisting it up a building and the device needed significant repairs. On flat terrain that didn’t provide any high spots, survey towers needed to be constructed, some of which still exist today, both so that surveyors can sight from them as well as to other points.
And don’t think that sighting these points was a simple affair either.
Triangulation points were often over 20 miles apart if terrain allowed, so you’d be using a telescope to pick out a small point in the distance. Even worse, in the earlier days, the spotting targets were opaque, unlit objects like flagpoles. The heliotrope, a telescope and mirror device that focuses and reflects the sun towards a point for easier survey spotting, would not be invented until 1821 and were not used in the India survey until 1832 after their introduction by Everest.
Prior to the heliotrope and other self-illuminating spotting targets, surveying was often done in the rainy season because the visibility and atmospheric distortions due to temperature and weather were at a minimum then. Surveyors would have to drag all their equipment through the heavy monsoon rains, set up, and wait for the morning rains to end and make their observations, weather permitting. When the heliotrope was introduced, Everest expresses joy at having to not subject his subordinates from having to endure that “reckless waste of life and health”.

Some math-y, correction stuff
One thing to remember is that the Earth is round(ish). So the triangles in question aren’t perfectly flat triangles where all angles sum to 180 degrees. So there are also corrections for things like the curvature of the earth, refraction and distortion by the atmosphere, etc.. The records I examined didn’t mention much about these corrections because they were primarily devoted to the actual operations of taking the measurements. I’d expect the later volumes to cover the math involved.
Just keep measuring
Armed with these base-lines, theodolites, and tons of manpower, the people on this surveying project would continue on until the whole territory would be measured. The records of this project stretch multiple volumes, not all of which have been digitized. The digitized ones are available for examination since they’re old enough to be in the public domain now. I doubt I will ever have the time to even briefly skim through them all.
So to end, measuring a continent takes a lot of triangles, a ridiculous amount of resources, and a lot of trekking across the countryside in often miserable conditions. If anything it reminds me that for many things, the simple solutions do work and might be the only practical way to do something… if you have the resources and stamina to follow through.
Extra References I Used
A brief secondary summary of the Great Trigonometrical Survey that helped point me to references and put the broad story in my brain before I dove into the bigger references.
There are also a number of YouTube videos, I found this and this to be particularly interesting as I was just getting an idea of how surveying even works.
The Jesse Ramsden created many of the “Great Theodolites”, one of which was used in the survey of India. This paper by Insley details a number of these theodolites (of interest appear to be numbered 2 through 7), and mentions that some of the earlier designs used weighed around 200 pounds, but the one adopted in 1830 weighed around 1100 pounds when all the parts (including stand, etc) were brought together.
Standing offer: If you created something and would like me to review or share it w/ the data community — my mailbox and Twitter DMs are open.
About this newsletter
I’m Randy Au, Quantitative UX researcher, former data analyst, and general-purpose data and tech nerd. Counting Stuff is a weekly newsletter about the less-than-sexy aspects of data science, UX research and tech. With excursions into other fun topics.
Curated archive of evergreen posts can be found at randyau.com.
Join the Approaching Significance Discord, where data folk hang out and can talk a bit about data, and a bit about everything else.
All photos/drawings used are taken/created by Randy unless otherwise noted.
Supporting this newsletter:
This newsletter is free, share it with your friends without guilt! But if you like the content and want to send some love, here’s some options:
Tweet me - Comments and questions are always welcome, they often inspire new posts
A small one-time donation at Ko-fi - Thanks to everyone who’s sent a small donation! I read every single note!
If shirts and swag are more your style there’s some here - There’s a plane w/ dots shirt available!